Difference between revisions of "England-2011-lab1-yellow"
(→Lab PDF) |
|||
| (13 intermediate revisions by one other user not shown) | |||
| Line 1: | Line 1: | ||
__NOTOC__ | __NOTOC__ | ||
= Lab Write-up for Group Yellow = | = Lab Write-up for Group Yellow = | ||
| − | == Lab PDF == | + | == Lab + PDF version == |
| Line 10: | Line 10: | ||
| − | |||
| − | [[ | + | |
| + | [[Image:Photo1 1.JPG|thumb|left|alt=A cartoon centipede reads books and types on a laptop.|Picture 1 .]] | ||
| + | |||
| + | |||
| + | |||
| + | [[Image:Photo2 2.JPG|thumb|left|alt=A cartoon centipede reads books and types on a laptop.|Picture 2.]] | ||
| + | |||
| + | [[Image:Photo3 3.JPG|thumb|left|alt=A cartoon centipede reads books and types on a laptop.|Picture 3 .]] | ||
| + | |||
| + | |||
| + | |||
| + | [[Image:Photo4 4.JPG|thumb|left|alt=A cartoon centipede reads books and types on a laptop.|Picture 4 .]] | ||
| + | |||
| + | |||
| + | |||
| + | Group Report 1: Where am I? | ||
| + | Yellow team: Ivan, Mamus, and Vivian. | ||
| + | |||
| + | Our focus point was the distal end of Croom’s Hill Groove. We used three different methods/approach to identify our destination which includes Google earth, GPS and method of estimated (natural way). We used the GPS, Google earth, proximate measures, timer, camera and a compass as our tools. Below is a description of our identification by the use of longitude, latitude, elevation and distance. | ||
| + | |||
| + | Latitude: | ||
| + | GPS reading: 51.47728 | ||
| + | Google earth: 51.477543 | ||
| + | Estimation: | ||
| + | |||
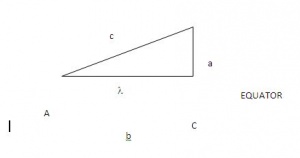
| + | <span style="color:#FFFFFF; background:#FF69B4"> PICTURE 1 </span> | ||
| + | |||
| + | |||
| + | Using Google Earth, we measured the distance from to the Equator to the closest approximate point to Croom’s Hill, Greenwich England. At this point we then used general knowledge (with a little help from Google) to establish the distance from the Earth’s core to the surface. Using the Pythagorean Theorem, we found the angle between AB and AC, which represents the an estimation of latitude for the purposes of this experiment. | ||
| + | |||
| + | In the diagram, | ||
| + | a= 3441.58 miles (distance from Equator to Greenwich, England | ||
| + | b=3975 miles (distance from Earth’s center to its surface) | ||
| + | c= side needed in order to complete equation finding angle of latitude. | ||
| + | |||
| + | c =sqr(1915^2 + 3975^2 | ||
| + | c =5257.860… | ||
| + | |||
| + | Finding A | ||
| + | |||
| + | A=sin(a/c) | ||
| + | A= sin(3441.58/5257.86) | ||
| + | A=.inverse of sin (.608) | ||
| + | A=37.45° | ||
| + | Therefore the angle of latitude using estimation is 37.45°. | ||
| + | |||
| + | Longitude: | ||
| + | GPS: 00.000765 | ||
| + | Google earth: 00.007876 | ||
| + | Estimation: | ||
| + | For every 15 ° of longitude, there is a 60 mins difference in time. We were 8 minutes away from the prime meridian of 0°, so our calculation of the longitude degree was as follows: | ||
| + | 15°=60mins | ||
| + | ???=8mins | ||
| + | (15*60)/8 | ||
| + | 2° | ||
| + | |||
| + | Elevation: | ||
| + | GPS: 18.5 ft but we changed this to 60ft through computer calculator. | ||
| + | Google earth: 59 ft | ||
| + | Estimation: | ||
| + | By the natural arm method, we estimated the angle from Greenwich to our destination to be 60°. As shown on the triangle below we used the cosine and Pythagorean theory to find our elevation. | ||
| + | |||
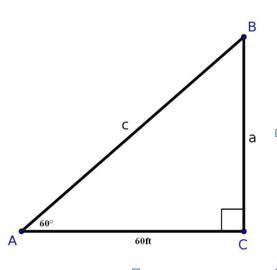
| + | <span style="color:#FFFFFF; background:#FF69B4"> PICTURE 2 </span> | ||
| + | |||
| + | |||
| + | AC/BC= Cos a° | ||
| + | |||
| + | 60ft/BC=Cos60° | ||
| + | |||
| + | BC= 60Cos60° | ||
| + | |||
| + | BC=60(0.5) | ||
| + | |||
| + | BC=30ft | ||
| + | |||
| + | a2+b2=c2 | ||
| + | |||
| + | 602+302=c2 | ||
| + | |||
| + | 3600+90=c2 | ||
| + | |||
| + | ?4500=c | ||
| + | |||
| + | C=67.08ft (our angle of elevation) | ||
| + | |||
| + | |||
| + | Distance: | ||
| + | Google earth: 540m | ||
| + | Estimation: | ||
| + | We used Ivan’s feet which we approximated to be 1 step is equivalent to 1 meter. Evan walked 10 steps in 07:48sec, which we approximated to be 8secs, so it takes one person to walk 10meters in 8 secs. We walked from our point (Croom’s Hill Grove) to in approximately 8 mins. So below are the calculations of the distance it took us from our point to the prime meridian. | ||
| + | |||
| + | 10meter=8seconds | ||
| + | ???=480seconds (8*60) | ||
| + | (10m*480s)/8s = 675m | ||
| + | |||
| + | Below are pictures of the North aside and a description. | ||
| + | |||
| + | North side description: | ||
| + | Narrow road | ||
| + | Houses in form of flats with tiles on the roof | ||
| + | Cars parked on the right side of the street, near houses. | ||
| + | |||
| + | |||
| + | <span style="color:#FFFFFF; background:#FF69B4"> PICTURE 3 </span> | ||
| + | |||
| + | South side description: | ||
| + | A garden | ||
| + | Garbage | ||
| + | Dead end with a small/shallow wall. | ||
| + | |||
| + | |||
| + | <span style="color:#FFFFFF; background:#FF69B4"> PICTURE 4 </span> | ||
| + | |||
| + | |||
| + | Weaknesses: | ||
| + | Time was not accurate, as it depends on ones pace of walking, the answer (time it took us to walk) could vary depending on one’s speed. | ||
| + | The GPS is not as accurate. Their accuracy will be within about 10 to 50 feet (3 to 15 meters), 95% of the time. | ||
| + | |||
| + | <span style="color:blue">Reviewed - 21 February 2011</span> | ||
Latest revision as of 17:36, 21 February 2011
Lab Write-up for Group Yellow
Lab + PDF version
Group Report 1: Where am I? Yellow team: Ivan, Mamus, and Vivian.
Our focus point was the distal end of Croom’s Hill Groove. We used three different methods/approach to identify our destination which includes Google earth, GPS and method of estimated (natural way). We used the GPS, Google earth, proximate measures, timer, camera and a compass as our tools. Below is a description of our identification by the use of longitude, latitude, elevation and distance.
Latitude: GPS reading: 51.47728 Google earth: 51.477543 Estimation:
PICTURE 1
Using Google Earth, we measured the distance from to the Equator to the closest approximate point to Croom’s Hill, Greenwich England. At this point we then used general knowledge (with a little help from Google) to establish the distance from the Earth’s core to the surface. Using the Pythagorean Theorem, we found the angle between AB and AC, which represents the an estimation of latitude for the purposes of this experiment.
In the diagram, a= 3441.58 miles (distance from Equator to Greenwich, England b=3975 miles (distance from Earth’s center to its surface) c= side needed in order to complete equation finding angle of latitude.
c =sqr(1915^2 + 3975^2 c =5257.860…
Finding A
A=sin(a/c) A= sin(3441.58/5257.86) A=.inverse of sin (.608) A=37.45° Therefore the angle of latitude using estimation is 37.45°.
Longitude: GPS: 00.000765 Google earth: 00.007876 Estimation: For every 15 ° of longitude, there is a 60 mins difference in time. We were 8 minutes away from the prime meridian of 0°, so our calculation of the longitude degree was as follows: 15°=60mins ???=8mins (15*60)/8 2°
Elevation: GPS: 18.5 ft but we changed this to 60ft through computer calculator. Google earth: 59 ft Estimation: By the natural arm method, we estimated the angle from Greenwich to our destination to be 60°. As shown on the triangle below we used the cosine and Pythagorean theory to find our elevation.
PICTURE 2
AC/BC= Cos a°
60ft/BC=Cos60°
BC= 60Cos60°
BC=60(0.5)
BC=30ft
a2+b2=c2
602+302=c2
3600+90=c2
?4500=c
C=67.08ft (our angle of elevation)
Distance:
Google earth: 540m
Estimation:
We used Ivan’s feet which we approximated to be 1 step is equivalent to 1 meter. Evan walked 10 steps in 07:48sec, which we approximated to be 8secs, so it takes one person to walk 10meters in 8 secs. We walked from our point (Croom’s Hill Grove) to in approximately 8 mins. So below are the calculations of the distance it took us from our point to the prime meridian.
10meter=8seconds ???=480seconds (8*60) (10m*480s)/8s = 675m
Below are pictures of the North aside and a description.
North side description: Narrow road Houses in form of flats with tiles on the roof Cars parked on the right side of the street, near houses.
PICTURE 3
South side description: A garden Garbage Dead end with a small/shallow wall.
PICTURE 4
Weaknesses:
Time was not accurate, as it depends on ones pace of walking, the answer (time it took us to walk) could vary depending on one’s speed.
The GPS is not as accurate. Their accuracy will be within about 10 to 50 feet (3 to 15 meters), 95% of the time.
Reviewed - 21 February 2011